miliprojects.blogg.se - Pca method for hyperimage

A simplified format is : PCA(X, scale.unit = TRUE, ncp = 5, graph = TRUE) It takes a numeric matrix as an input and performs the scaling on the columns. The R base function `scale() can be used to standardize the data. Where \(mean(x)\) is the mean of x values, and \(sd(x)\) is the standard deviation (SD). When scaling variables, the data can be transformed as follow: We might also want to scale the data when the mean and/or the standard deviation of variables are largely different. The standardization of data is an approach widely used in the context of gene expression data analysis before PCA and clustering analysis. Generally variables are scaled to have i) standard deviation one and ii) mean zero. The goal is to make the variables comparable. This is particularly recommended when variables are measured in different scales (e.g: kilograms, kilometers, centimeters, …) otherwise, the PCA outputs obtained will be severely affected. In principal component analysis, variables are often scaled (i.e. standardized). Head(decathlon2.active, 4) # X100m Long.jump Shot.put High.jump X400m X110m.hurdle We start by subsetting active individuals and active variables for the principal component analysis: decathlon2.active <- decathlon2 It can be used to color individuals by groups. This is a categorical (or factor) variable factor. Supplementary qualitative variables (green): Column 13 corresponding to the two athlete-tic meetings (2004 Olympic Game or 2004 Decastar).Supplementary continuous variables (red): Columns 11 and 12 corresponding respectively to the rank and the points of athletes.

Supplementary variables: As supplementary individuals, the coordinates of these variables will be predicted also.

Active variables (in pink, columns 1:10) : Variables that are used for the principal component analysis.

Supplementary individuals (in dark blue, rows 24:27) : The coordinates of these individuals will be predicted using the PCA information and parameters obtained with active individuals/variables.

Active individuals (in light blue, rows 1:23) : Individuals that are used during the principal component analysis.

Due to this redundancy, PCA can be used to reduce the original variables into a smaller number of new variables ( = principal components) explaining most of the variance in the original variables. Correlation indicates that there is redundancy in the data. Note that, the PCA method is particularly useful when the variables within the data set are highly correlated. Technically speaking, the amount of variance retained by each principal component is measured by the so-called eigenvalue. The dimensionality of our two-dimensional data can be reduced to a single dimension by projecting each sample onto the first principal component (Plot 1B) The PC2 axis is the second most important direction and it is orthogonal to the PC1 axis. In the figure below, the PC1 axis is the first principal direction along which the samples show the largest variation. PCA assumes that the directions with the largest variances are the most “important” (i.e, the most principal). The dimension reduction is achieved by identifying the principal directions, called principal components, in which the data varies.

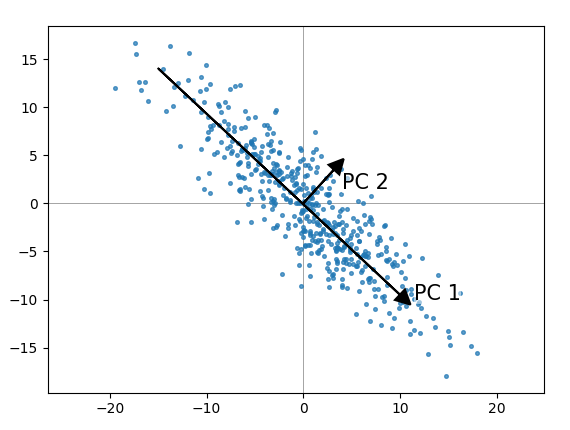
In the Plot 1A below, the data are represented in the X-Y coordinate system. Here, we’ll explain only the basics with simple graphical representation of the data. Understanding the details of PCA requires knowledge of linear algebra. In other words, PCA reduces the dimensionality of a multivariate data to two or three principal components, that can be visualized graphically, with minimal loss of information. The goal of PCA is to identify directions (or principal components) along which the variation in the data is maximal. The information in a given data set corresponds to the total variation it contains. The number of principal components is less than or equal to the number of original variables. These new variables correspond to a linear combination of the originals. Principal component analysis is used to extract the important information from a multivariate data table and to express this information as a set of few new variables called principal components. If you have more than 3 variables in your data sets, it could be very difficult to visualize a multi-dimensional hyperspace. Each variable could be considered as a different dimension. Principal component analysis ( PCA) allows us to summarize and to visualize the information in a data set containing individuals/observations described by multiple inter-correlated quantitative variables.